Variational approach to the analysis of massive data arrays
Visual images, signals, symbolic sequences, as well as sets and successions o f images, signals or symbolic sequences, these all are glowing examples of massive ordered data sets. A bulk of data analysis problems for such a kind of data lend themselves to mathematical formulation as variational (optimization) problems with the so-called separable objective functions, i.e. those ones which consist of additive constituents of only one or two arguments. The aim of the research is constructing effective generalized data analysis algorithms on the basis of decomposition of the original optimization problem into a succession of intervening problems with tree-like and chain-like separability of partial objective functions. The generalized data analysis procedure is based on an extension of the classical dynamic programming procedure onto the case of tree-like adjacency of goal variables.

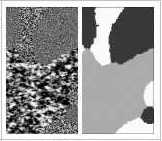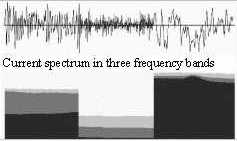
Edge-preserving time-frequency analysis of signals	Segmentation of texture images

Robust forming of feature spaces and decision rules for the recognition of signals of different length
The natural space of the initial signal representation is that formed by succession of the signal’s samples along the discrete axis of the respective variable, primarily, time. Forming decision rules of signal recognition is concerned with two fundamental barriers. First, the dimensionality of the feature space is, as a rule, individual for each particular signal, so, there is no common space in which a discriminant function could be sought for. Second, the feature-space dimensionality is practically ever much greater than the number of signals in the training set, what turns the training problem into an ill posed one. The theoretical research is aimed at overcoming both of these difficulties when inferring a decision rule from a training set.

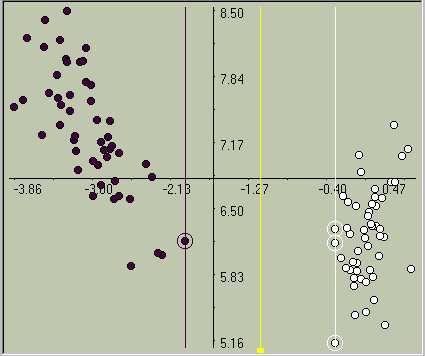
Two-dimensional representation of a training set of high-dimensional vectors of signal samples, and the optimal linear decision rule approximately distinguishing between two slightly intersecting classes of signals.